Menghitung Besar dan Arah Resultan Vektor

Terdapat beberapa metode untuk menghitung besar resultan vektor dan arah resultan vektor, metode-metode tersebut menggunakan dasar trigonometri dan rumus sinus-kosinus untuk menyelesaikan soal-soal vektor, berikut ini adalah cara menghitungnya:

1. Menggunakan Aturan (Rumus) Kosinus
Untuk menghitung resultan vektor pada sembarang sudut, maka kita dapat menggunakan rumus kosinus, yaitu:
\(a^2 = b^2 + c^2 - 2.b.c.\cos A\)

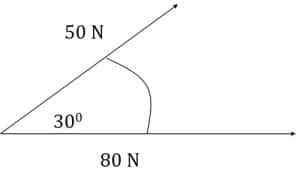
Misalnya terdapat dua buah vektor 50N dan 80N yang membentuk sudut \(180^{\circ} - A = 30^{\circ}\) seperti pada gambar di bawah ini, tentukan besar dan arah resultan vektor.

Pertama-tama, untuk dapat menggunakan aturan kosinus, kita harus memodifikasi segitiga tersebut menjadi seperti gambar di bawah ini. Lalu gunakan aturan kosinus:

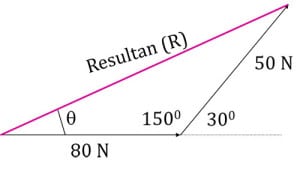
\(R^2 = b^2 + c^2 - 2.b.c.\cos A\)
\(R^2 = 80^2 + 50^2 - 2.80.50.\cos 150^{\circ}\)
\[R^2 = 6400 + 2500 - 8000.(-\frac{1}{2}\sqrt{3})\] \(R^2 = 15828,2 \Rightarrow R = 125,8 N\)

Gunakan aturan sinus untuk mencari sudut \(\theta\):
\[\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}\] \[\frac{\sin \theta}{50} = \frac{\sin 150^{\circ}}{125,8}\] \(25 = 125,8.\sin \theta \Rightarrow \theta = 11,46^{\circ}\)

2. Menggunakan Aturan (Rumus) Kosinus Modifikasi*
Rumus ini sering disebut dengan metode jajar genjang, dengan menyederhanakan aturan kosinus untuk memudahkan kita dalam mengerjakan soal dua buah resultan yang membentuk sudut apit \(\alpha\).

Pada soal yang sama, misalnya terdapat dua buah vektor 50N dan 80N yang membentuk sudut \(\alpha = 30^{\circ}\) seperti pada gambar di bawah ini, tentukan besar dan arah resultan vektor.

Pertama-tama, untuk dapat menggunakan aturan kosinus*, kita harus memodifikasi segitiga tersebut menjadi seperti gambar di bawah ini. Lalu gunakan aturan kosinus*:

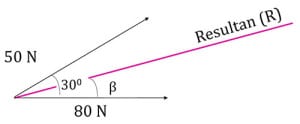
\(R^2 = {V_1}^2 + {V_2}^2 + 2.V_1.V_2.\cos \alpha\)
\(R^2 = 50^2 + 80^2 + 2.50.80.\cos 30^{\circ}\)
\[R^2 = 2500 + 6400 + 8000.\frac{1}{2}\sqrt{3}\] \(R^2 = 15828,2 \Rightarrow R = 125,8 N\)

Gunakan aturan sinus* untuk mencari sudut \(\beta\):
\[\frac{R}{\sin \alpha} = \frac{V_2}{\sin \beta}\] \[\frac{125,8}{0,5} = \frac{50}{\sin \beta}\] \(25 = 125,8.\sin \beta \Rightarrow \beta = 11,46^{\circ}\)

Perhatikan bahwa rumus trigonometri yang digunakan bergantung pada segitiga yang kita pakai untuk menghitung. Walaupun hasilnya sama, namun tiap siswa mungkin memiliki kesukaan tersendiri pada rumus tertentu untuk menghitung besar dan resultan vektor.

3. Memisahkan Komponen Vektor
Cara ini mungkin adalah cara yang paling intuitif untuk digunakan, dan sering digunakan untuk perhitungan fisika yang lain, namun cara ini memiliki kekurangan yaitu membutuhkan waktu yang lebih lama. Kelebihan cara ini adalah dapat digunakan untuk lebih dari 2 vektor.

Pada soal yang sama, misalnya terdapat dua buah vektor 50N dan 80N yang membentuk sudut \(\alpha = 30^{\circ}\) seperti pada gambar di bawah ini, tentukan besar dan arah resultan vektor.

Mari kita tinjau komponen pada sumbu-x dan sumbu-y:

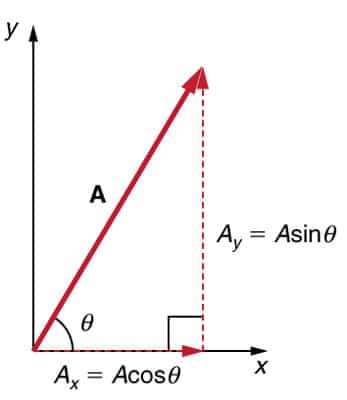
Pada sumbu-x
\(V_{1x} = V_1.\cos \alpha\)
\[V_{1x} = 50.\frac{1}{2}\sqrt{3}\] \(V_{1x} = 43,3N\)

\(V_{2x} = V_2.\cos0^{\circ}\)
\(V_{2x} = 80N\)
\(R_x = 43,3 + 80 = 123,3 N\)

Pada sumbu-y
\(V_{1y} = V_1.\sin \alpha\)
\[V_{1y} = 50.\frac{1}{2}\] \(V_{1y} = 25N\)

\(V_{2y} = V_2.\sin 0^{\circ}\)
\(V_{2y} = 0N\)

\(R_y = 25 + 0 = 25 N\)

Besar Resultan dihitung menggunakan teorema pythagoras:

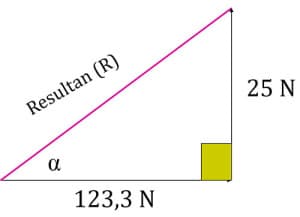
\(R = \sqrt{{R_x}^2 + {R_y}^2}\)
\(R = \sqrt{{123,3}^2 + {25}^2}\)
\(R = 125,8 N\)

Arah Resultan dihitung menggunakan tangen
\[\tan\alpha = \frac{R_y}{R_x}\] \[\tan\alpha = \frac{25}{123,3}\] \(\alpha = 11,46^{\circ}\)

Inilah cara menghitung besar dan arah resultan vektor, apabila ada pertanyaan silahkan langsung menuju forum 🙂