Pada artikel yang lalu kita sudah membahas mengenai gerak lurus, sekarang kita akan membahas gerak melingkar. Gerak melingkar beraturan atau uniform circular motion adalah gerak objek pada lintasan lingkaran dengan kelajuan tetap atau percepatan nol.
Misalnya kita memutar benda bermassa tertentu pada seutas tali, maka terdapat beberapa besaran yang dapat kita analisis. Besaran-besaran pada gerak melingkar mirip dengan gerak lurus karena keduanya memiliki filosofi yang sama. Berikut ini adalah perbandingannya: [1]
Perbandingan Besaran Linier dan Rotasional
| Besaran linier/translasional | Besaran angular/rotasional |
|---|---|
| Perpindahan, posisi: \(x \ (m)\) | Perpindahan angular, sudut: \(\theta \ (rad)\) |
| Kecepatan: \(\mathbf{v} \ (m/s)\) | Kecepatan angular / kecepatan sudut: \(\omega \ (rad/s)\) |
| Percepatan: \(\mathbf{a} \ (m/s^2)\) | Percepatan angular / percepatan sudut: \(\alpha \ (rad/s^2)\) |
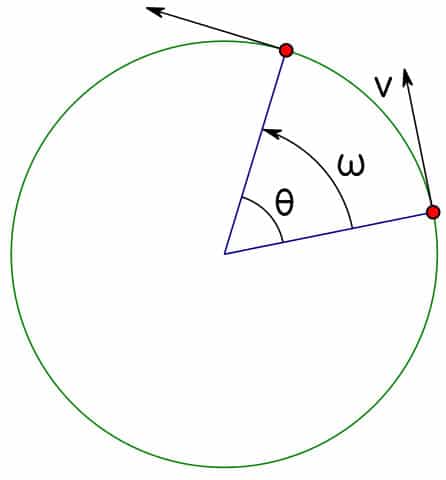
Ingat:
- \(\theta\) adalah besar sudut lintasan melingkar yang ditempuh.
- \(\omega\) adalah kecepatan sudut dengan arah melingkar.
- \(\alpha\) adalah percepatan sudut dengan arah melingkar.
Lalu bagaimana hubungan antar besaran rotasional pada GMB?
- \(\omega = \frac{\Delta \theta}{\Delta t}\)
- \(\alpha = \frac{\Delta \omega}{\Delta t}\)
Lalu bagaimana hubungan besaran rotasional dengan besaran linier pada GMB?
- \(x = \theta \ r\)
- \(v = \omega \ r\)
- \(a = \alpha \ r\)
dimana \(r\) adalah jari-jari lintasan lingkaran.
Kelajuan linier atau kelajuan tangensial (\(v\))
\(v\) adalah kelajuan linier atau kelajuan tangensial. Misalnya kita memutar bola pada seutas tali, ketika tiba-tiba tali putus maka bola itu akan bergerak tidak lagi melingkar tetapi menjadi lurus, arahnya tegak lurus (tangensial).
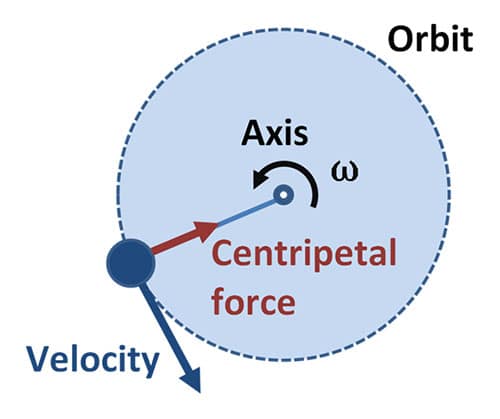
Percepatan sentripetal (\(a_s\))
Kita tahu menurut hukum newton pertama: "Sebuah benda yang bergerak akan tetap bergerak dengan kelajuan dan arah yang sama, kecuali mendapatkan gaya dari luar." Gaya yang membuat lintasan benda yang diputar berubah arah secara melingkar adalah gaya sentripetal \(F_s\) yang arahnya menuju pusat lingkaran. Ingat komponen gaya adalah massa dan percepatan, sehingga percepatan yang arahnya menuju pusat lingkaran adalah percepatan sentripetal (\(a_s\)).
\[a_s \ = \ {\omega}^2 \ r \ = \ \frac{v^2}{r}\]
Sebelum mengerjakan soal gerak melingkar beraturan, mari kita lihat video tentang gaya sentripetal sebentar.

Mari kita selesaikan contoh soal gerak melingkar beraturan berikut ini
1. Sebuah benda bergerak dengan kelajuan tetap \(v\) melalui lingkaran berjari-jari \(r\) dengan percepatan sentripetal \(a_s\).
a) agar percepatan sentripetalnya menjadi dua kali semula, maka?
b) Apabila \(v\) dijadikan 4 kali semula dan \(r\) dijadikan 2 kali semula, maka \(a_s\) menjadi?
a) Gunakan hukum kesebandingan
Mari kita tinjau dari hubungan pertama:
- \(a_s={\omega}^2 \ r\)
Sehingga
- \(a_s \propto {\omega}^2\) dan \(a_s \propto r\)
Agar \(a_s\) menjadi dua kali semula, maka \(r\) dapat dijadikan dua kali semula dengan menahan \(\omega\) tetap, atau \(\omega\) dijadikan \(\sqrt{2}\) kali semula dengan menahan \(r\) tetap.
Mari kita tinjau dari hubungan kedua:
- \(a_s = \frac{v^2}{r}\)
Sehingga
- \(a_s \propto v^2\) dan \(a_s \propto \frac{1}{r}\)
Agar \(a_s\) menjadi dua kali semula, maka \(r\) dapat dijadikan setengah kali semula dengan menahan \(v\) tetap, atau \(v\) dijadikan \(\sqrt{2}\) kali semula dengan menahan \(r\) tetap.
b) Gunakan hubungan kedua
- \(\frac{4^2}{2} \ = \ 8\)
- maka \(a_s\) menjadi 8 kali semula.
2. Sebuah kipas dengan jari-jari 10cm berputar pada 150rpm. Hitunglah kecepatan sudut dan kelajuan liniernya!
Diketahui:
- \(r \ = \ 10 \ cm \ = \ 0,1 \ m\)
- putaran \(150 \ rpm\)
Ditanya: \(\omega\) dan \(v\)
Jawab:
Kita dapat menghitung kelajuan linier dengan menghitung berapa total jarak tempuh dibagi dengan waktu untuk menempuhnya, rpm = rotasi per menit = rotasi per 60 detik, maka:
- \(v \ = \ 150 \ rpm \ = \ \frac{150.0,1 \ m \ .2\pi}{60s} \ = \ 0,5\pi \ m/s\)
Untuk mencari \(\omega\), menggunakan persamaan:
- \(\omega \ = \ \frac{v}{r} \ = \ \frac{0,5\pi}{0,1} \ = \ 5\pi \ rad/s\)
Atau
Dapat menghitung kecepatan sudut dahulu dengan menghitung berapa panjang lintasan melingkar (dalam radian) yang ditempuh dibagi dengan waktu untuk menempuhnya.
- \(\omega \ = \ 150 \ rpm \ = \ \frac{150.2\pi \ rad}{60s} \ = \ 5\pi \ rad/s\)
Kutip materi pelajaran ini:
Kontributor Tentorku, 2015, https://www.tentorku.com/gerak-melingkar-beraturan-gmb/ (diakses pada 13 Jul 2025).
Materi pelajaran ini bukan yang Anda butuhkan?
Anda bisa mengirimkan saran pada Tentorku di akun fb/twitter/google kami di @tentorku.
Topik dengan voting komentar terbanyak akan mendapatkan prioritas dibuatkan pembahasan.